Geek Mexicain

Vous faites partie de ceux qui pensent qu'une connexion web sécurisée (HTTPS dans l'URL pour les plus terre-à-terre d'entre nous, ou pire encore, le petit cadenas vert de votre navigateur) est inviolable ? Cet article est fait pour vous.

C'est un post publié sur le journal du CNRS qui nous a interpellé. Il semblerait que la liste de nombres premiers, étant l'essence même de la plupart des algorithmes de chiffrement actuels, aurait pu être altérée de par le passé, laissant la possibilité à de très grandes entités s'occupant de la sécurité intérieure des États (dont on ne citera bien entendu pas le nom), d'espionner de manière aisée les communications... même chiffrées d'une extrémité à une autre.

Mais une petite explication s'impose. Pour cela nous allons revenir sur l'algorithme de Diffie-Helman, servant, entre autre, au protocole de chiffrement SSL / TLS [which stands for Secure Sockets Layer / Transport Layer Security]. C'est le protocole ajoutant l'aspect secure à HTTP, qui a donné naissance au HTTPS.

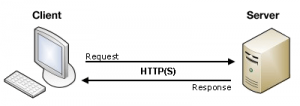
Pour cela, une configuration simple, que l'on retrouve d'ailleurs dans n'importe quel échange client / serveur: vous désirez faire parvenir un message de manière sécurisée à votre correspondant, que l'on appellera Carlos pour les besoins de la démonstration. Ajoutons un peu de piment (comme sur le logo du site) à cette illustration: James veut intercepter et déchiffrer ce message.

Étape n°0: Comprendre ce que je vais tenter d'expliquer. Pour cela, un petit point syntaxe: quand il sera écrit: X = a^b [c], signifie que X vaudra a mis à la puissance b (c'est bien tu nous a pris pour des incompétents ?), le tout modulo c. C'est-à-dire que a^b sera divisé par c, et que X prendra la valeur du reste de la division Euclidienne.

Étape n°1: Vous tirez un nombre premier p (c'est-à-dire divisible que par 1 et par lui même), et très très grand, de façon "aléatoire", dans une liste pré-établie. Ici, pour simplifier, nous allons prendre p = 17.

Étape n°2: Vous choisissez un nombre g appelé "base". Pour les besoins de l'explication, nous allons prendre g = 8.

Étape n°3: Maintenant vous tirez un nouveau nombre a (par exemple encore, ici a = 5), et vous calculer A = g^a [p], donc dans notre cas: A = 9.

Étape n°4: Vous envoyez maintenant à Carlos p, g et A. Une fois réceptionnés, Carlos choisit un nouveau nombre secret de son côté (b = 7 admettons), et calcule à son tour B = g^b [p], ce qui donne B = 15.

Étape n°5: Carlos vous fait parvenir son résultat B, et maintenant vous êtes capable de calculer finalement K = B^a [p], ce qui vaut K = 2. MAIS ! Magie, magie: de son côté Carlos calcule K' = A^b [p], ce qui lui donne... K' = 2.

Voilà, vous et votre correspondant avez réussis à convenir d'un secret, que même James (en ayant surveillé attentivement vos échanges encore non-chiffrés au début) ne peut pas arriver à retrouver (grâce à la puissance des mathématiques et du Groupe formé par les nombres premiers) ! En fait non, c'est inexact. En théorie, il pourrait parvenir à retrouver ce secret, mais il lui faudrait des mois (voire des années), car, si les nombres choisis sont assez grands, les opérations nécessaires prendraient un temps et une puissance de calcul monumentaux.

Alors si ce système est infaillible, pourquoi écrire un pareil article ? Bien vu ! Il se trouve que, comme présenté plus haut, un problème résiderait au niveau des nombres premiers tirés. Et oui, ils jouent un rôle très important dans ces calculs. Ce sont en grande partie grâce à eux que les opérations menées par Carlos et vous-même sont rendues quasiment unilatérales.

... et même ces nombres là ne sont pas assez "grands".

Toujours d'après le journal du CNRS, des informaticiens auraient prouvé que certains nombres premiers rendaient cet algorithme quasiment inutile, car le secret pourrait être cracké instantanément. Mais alors, qu'est-ce qui se passerait si ces dits nombres se retrouvaient dans une, ou plusieurs, des listes que nos programmes utilisent au quotidien ? Et pourtant, il serait très probable que nous vivions cela actuellement...

Pour finir, et en guise de "raison" à tout cela, on soulignera et retiendra quand même ces deux phrases magiques du journal du CNRS:

On note toutefois qu’une des listes [de nombres premiers] couramment utilisées a été établie par un sous-traitant de la NSA. Et que le scientifique à l’origine de la méthode utilisée par le groupe franco-américain, Daniel Gordon, travaille également pour une entreprise proche de cette même agence.

Et c'est pas moi qui l'ait dit ! À bon entendeur...